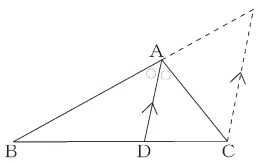
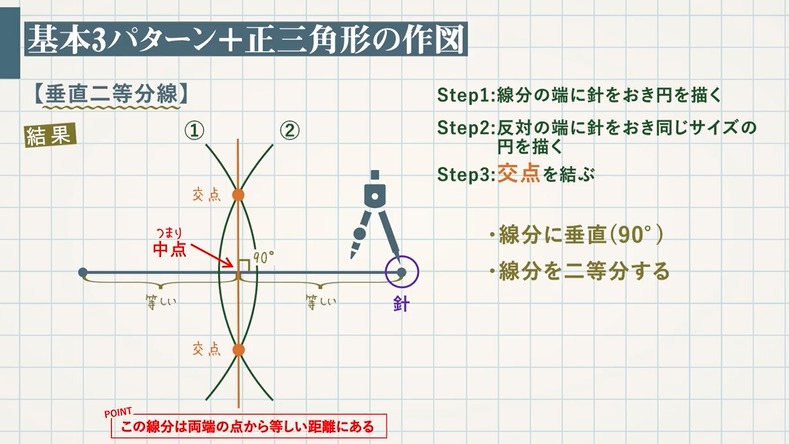
直線上の1点を通る垂線の作図 点C(直線上にある)を中心とする円をかき、直線ABとの交点をそれぞれP、Qとします 線分PQの両端の点を、それぞれ中心にして等しい半径の円をかき、交点をRとします 直線CRをひきましょう よく見てみると ②③は 「垂直
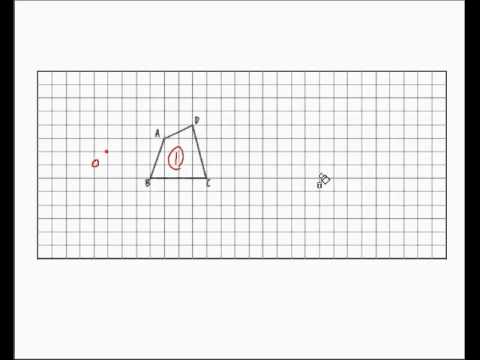
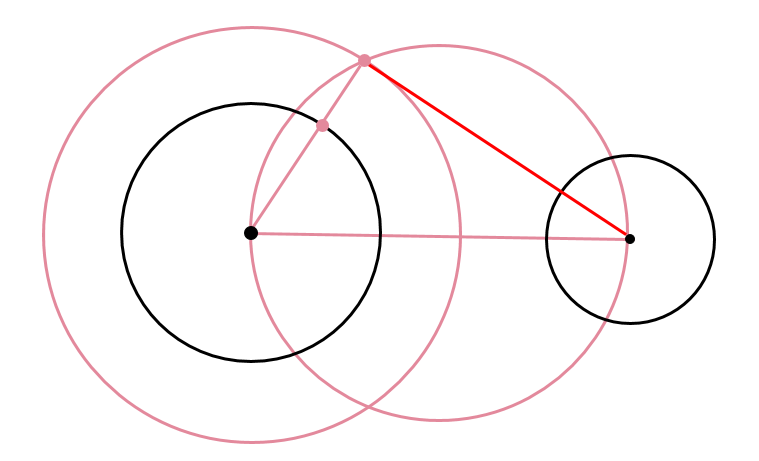
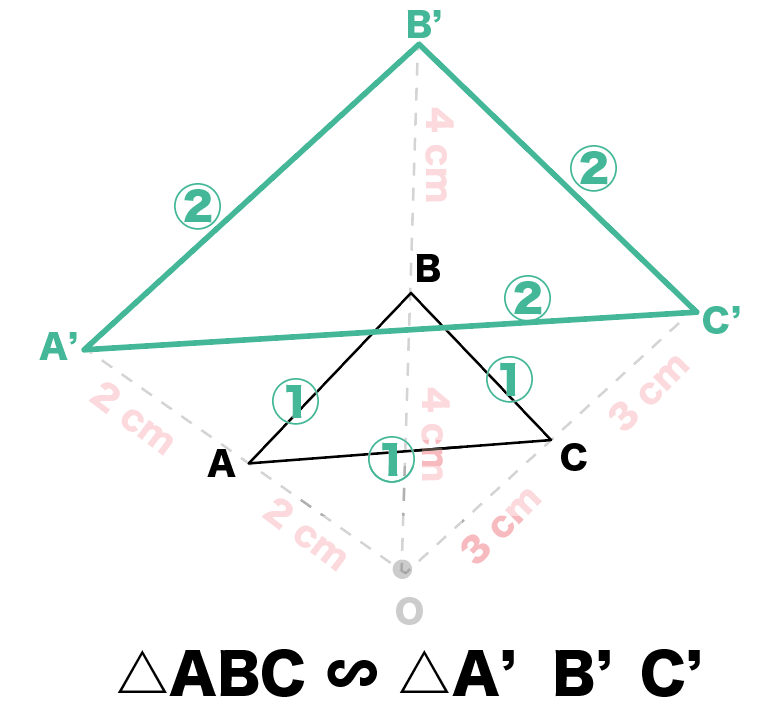
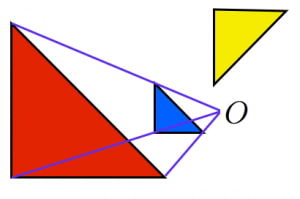
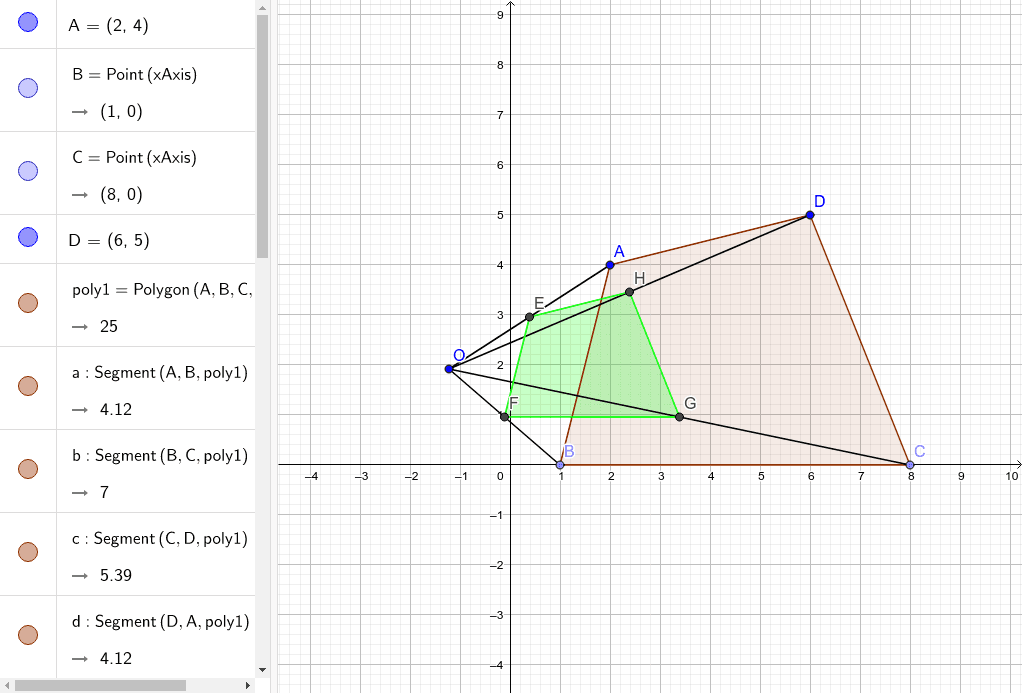
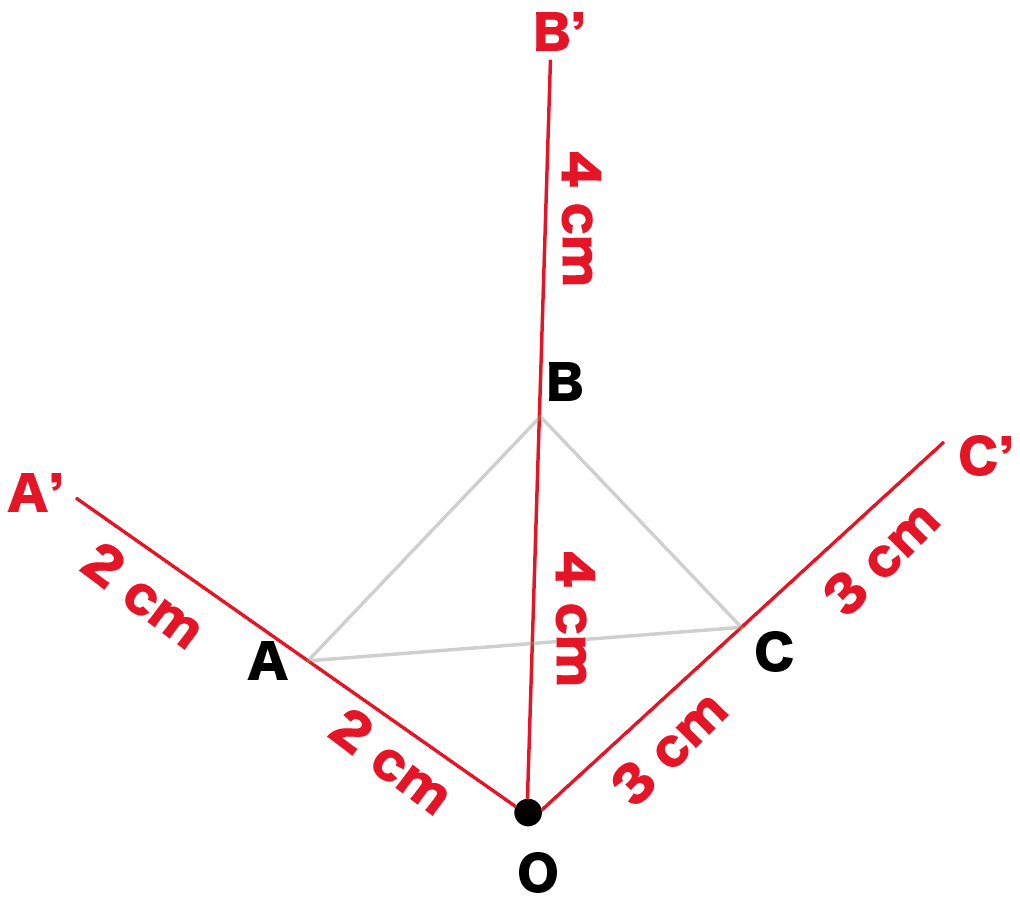
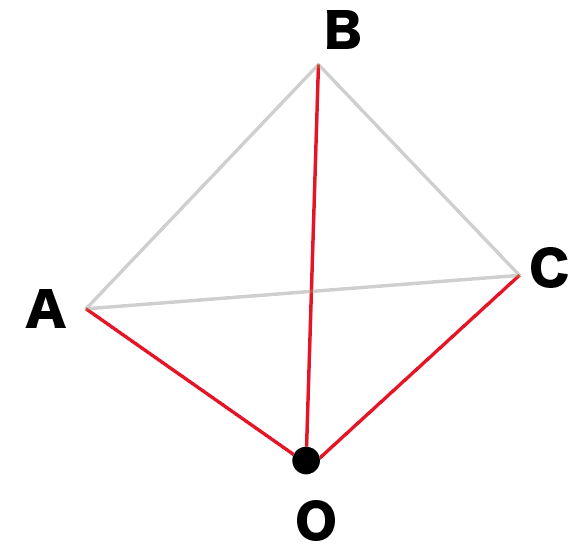
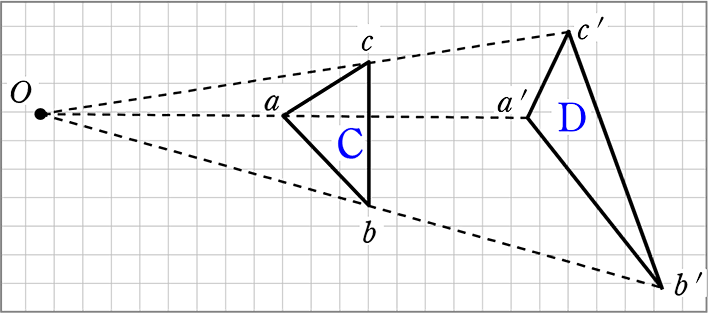
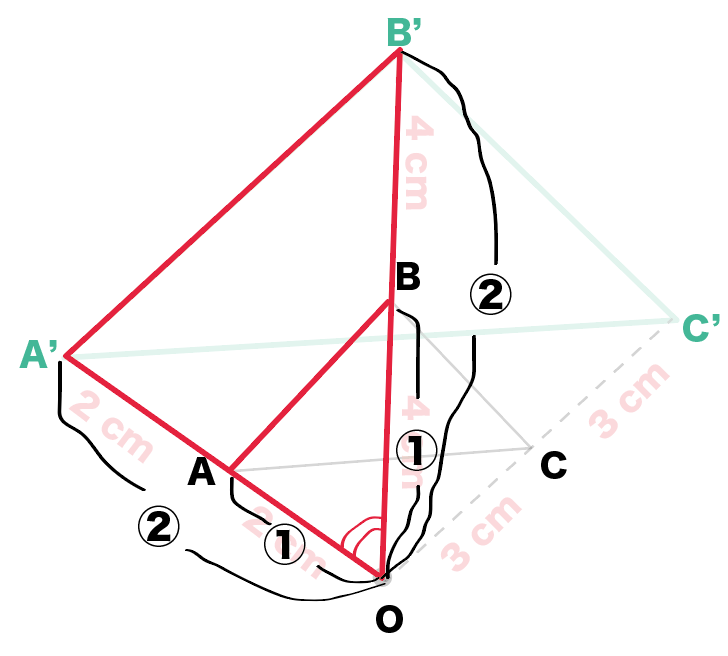
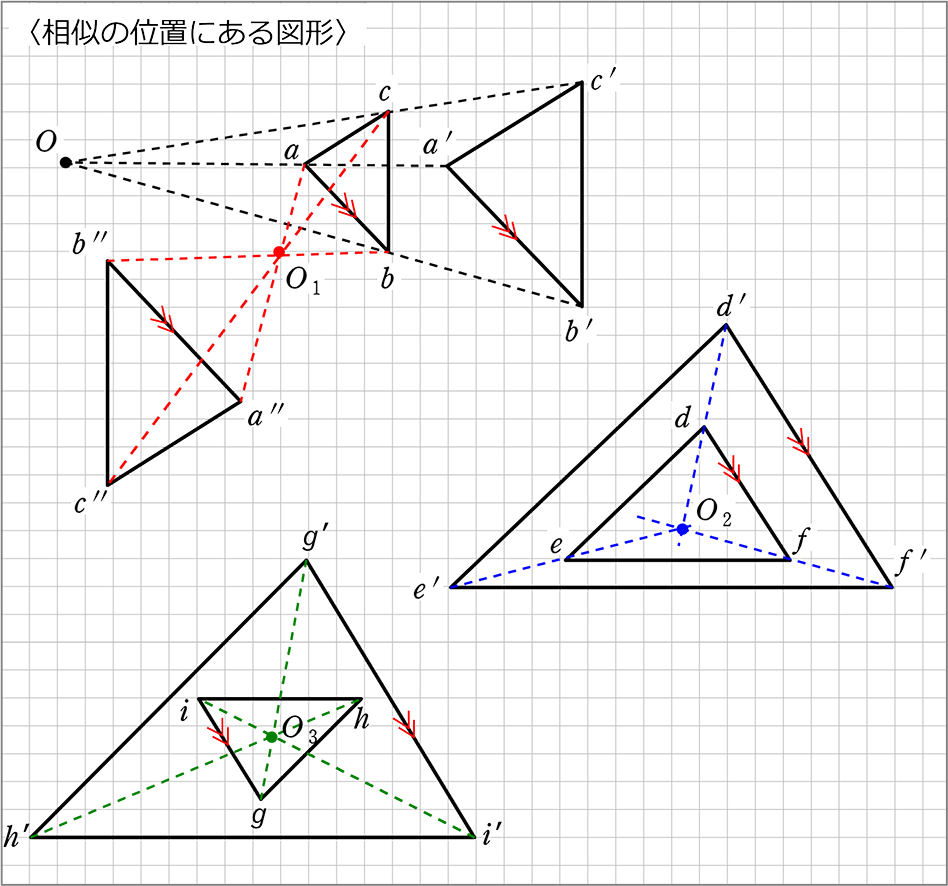
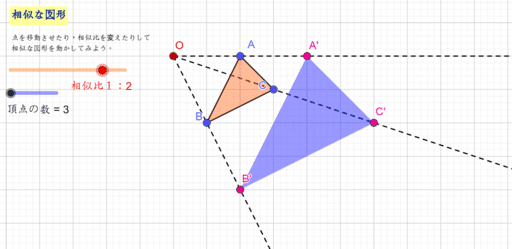
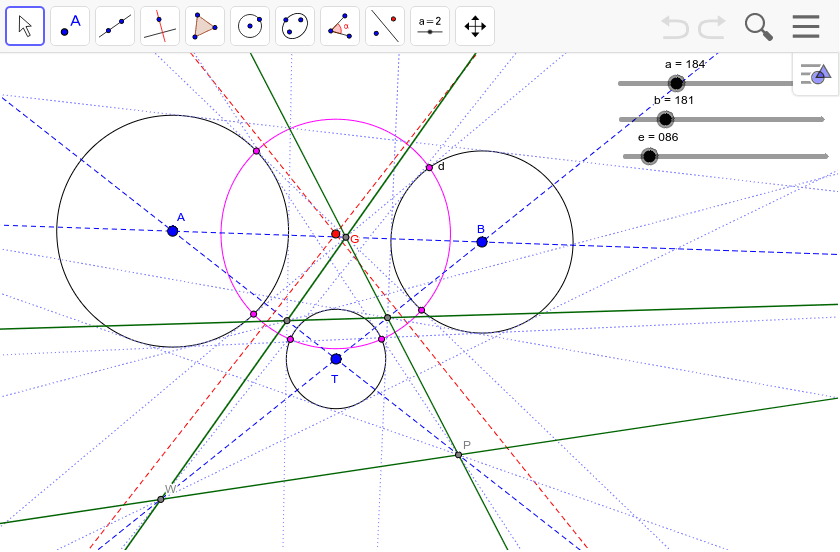
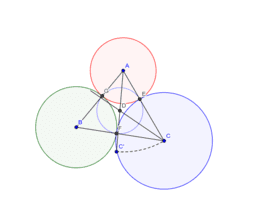
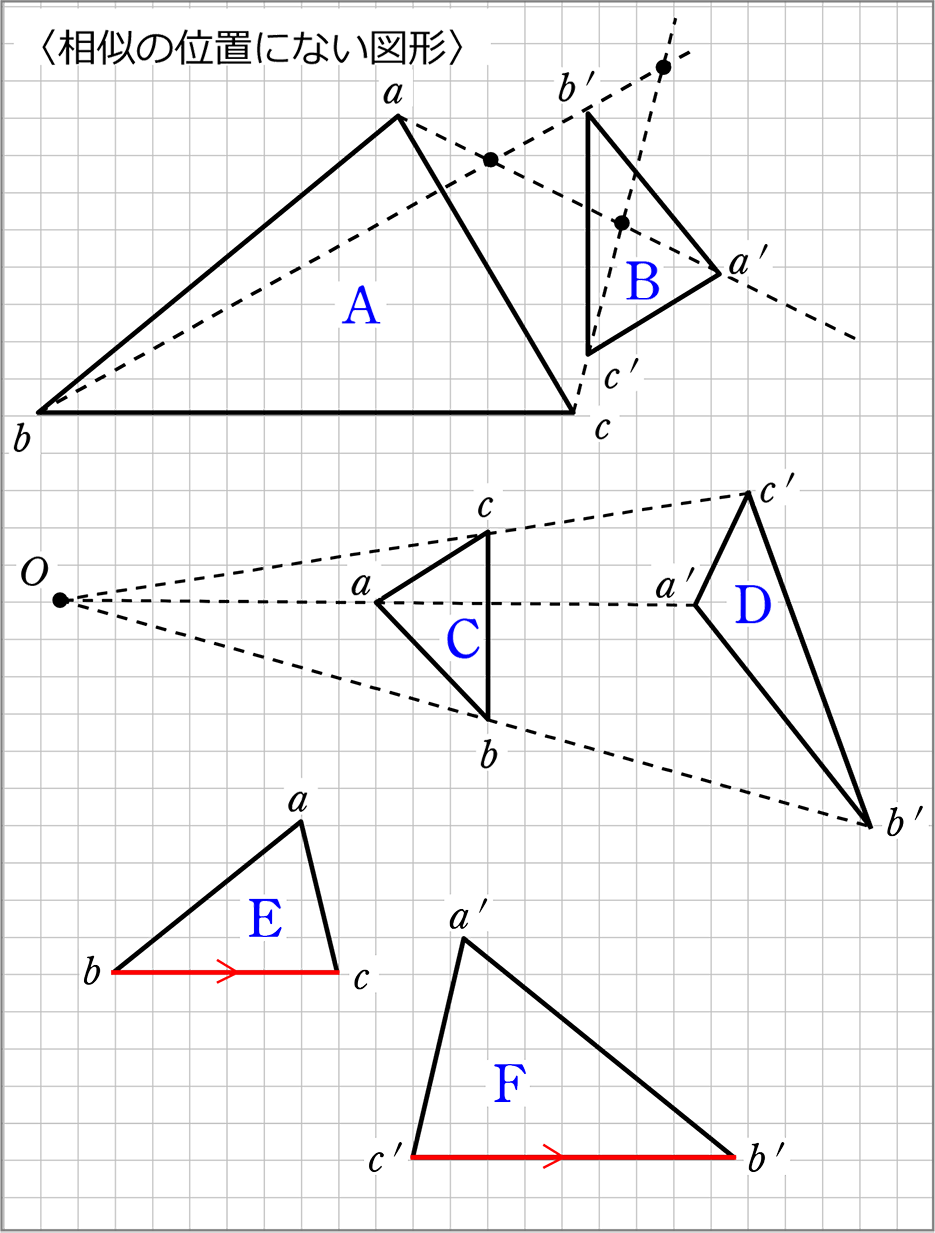
相似の中心 作図-点B'、C'を中心に半径B'A(=C'A)の円を描き、A以外の交点をOとすれば、これが求める中心です。 ⊿PAB'、⊿OAB'は共に2等辺三角形で底角Aが共通なので相似です。 後は省略します! これは、定規とコンパスを使った作図より、線を描く回数が少ないアポロニウスの問題(英 Problem of Apollonius)とは、平面において与えられた3つの円に接する円を描く問題である。とても面白い問題で、普通は8本あるが、いくつあるのかをフリーハンドで作図す
相似の中心 作図のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  | |
 |  | |
 |  |  |
「相似の中心 作図」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
 |  | |
「相似の中心 作図」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
 |  | |
「相似の中心 作図」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「相似の中心 作図」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「相似の中心 作図」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 | ||
 |  |  |
「相似の中心 作図」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「相似の中心 作図」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
 | ||
「相似の中心 作図」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |
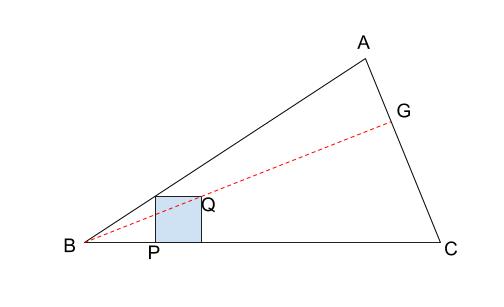
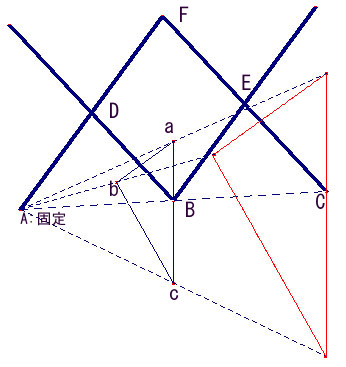
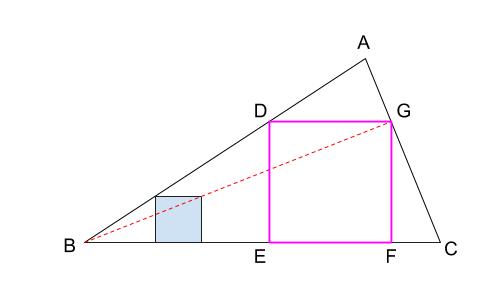
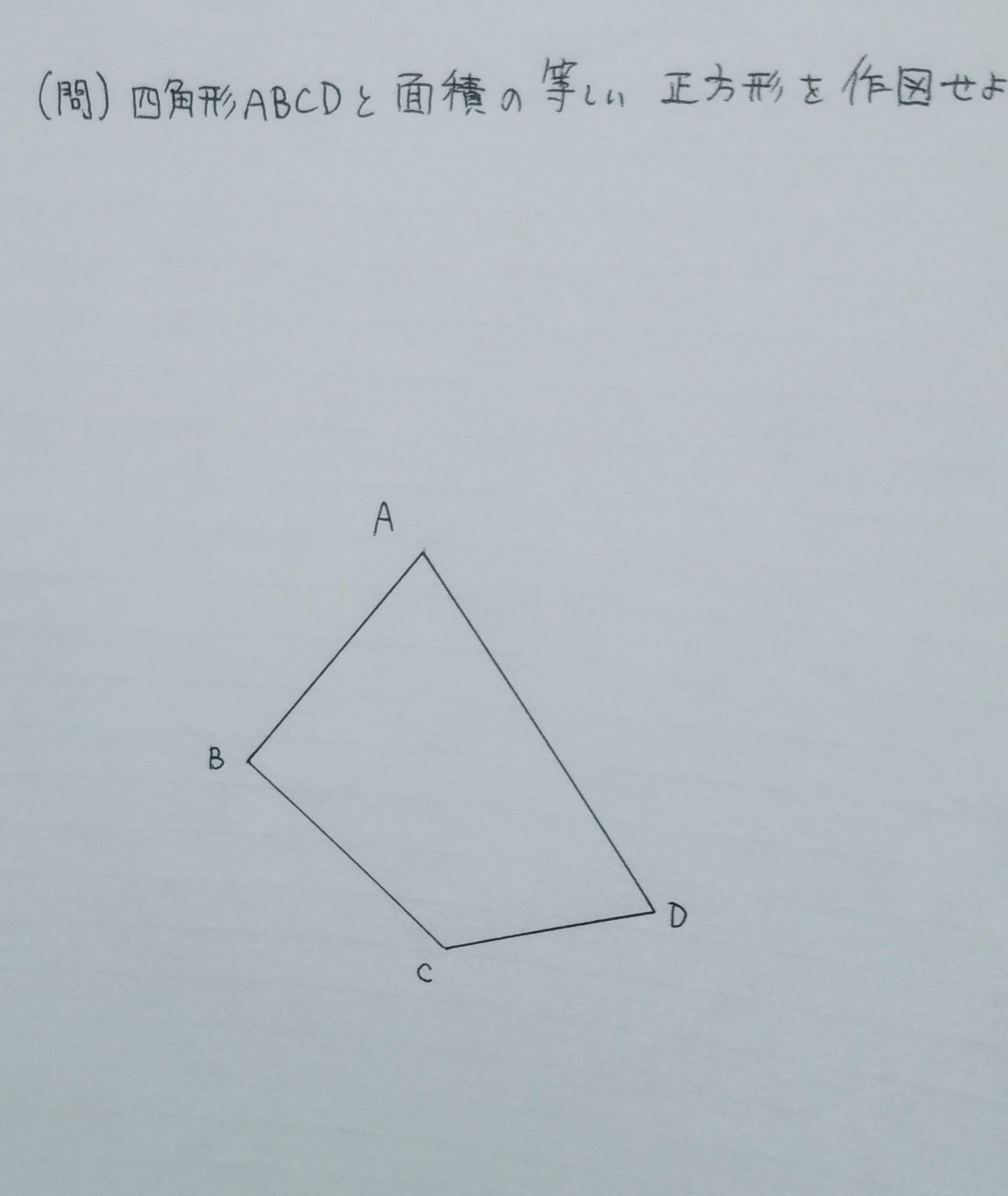
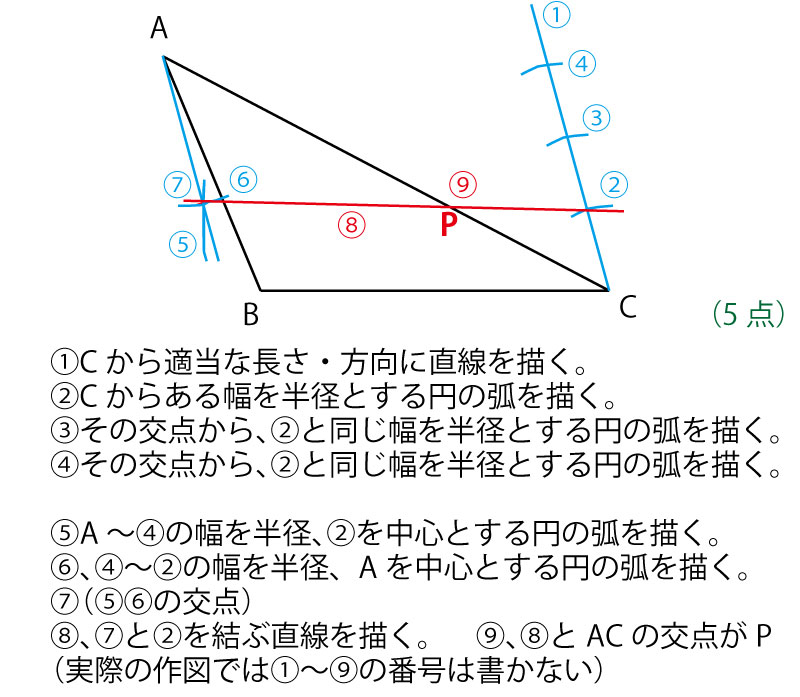
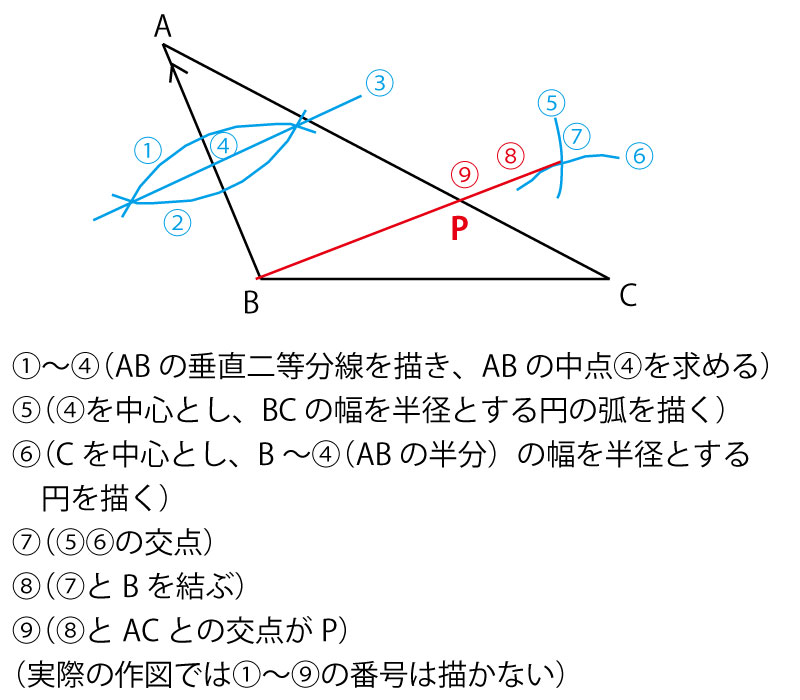
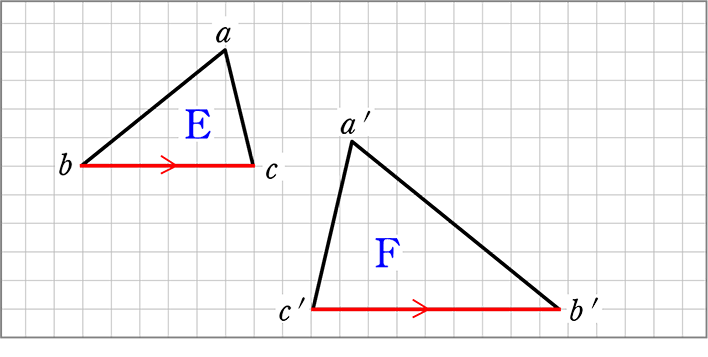
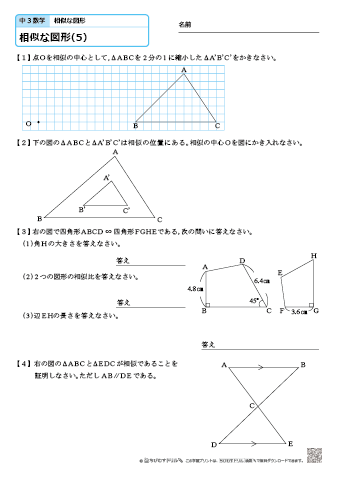
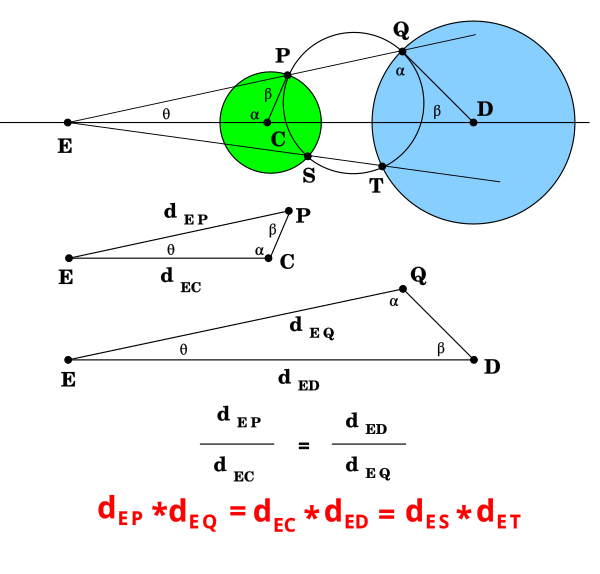
相似変換の不動点 西山豊 〒 大阪市東淀川区大隅228 大阪経済大学 経営情報学部 Tel EMail nishiyama@osakaueacjp 「数学を楽しむ/相似変換の不動点」『理系への数学』08年2月 Vol42, No11, 47に掲載 1.ランダムドット・パターン作図の方針は、相似の中心の利用です。 下図が作図の全容です。 水色の小さい正方形と、赤い正方形 DEF G D E F G が相似です。 点 B B が相似の中心となっています。 つまり、 水色の正方形を作図すれば、 点 G G の位置が確定できるのです。 あとは、これを作図していくのみです。 まずは水色の正方形を作図します。 BP B P の長さはいくつでもかまいません。 点 P P を通る BC B C の垂線の作図
Incoming Term: 相似の中心 作図, 相似の中心 作図 縮図,




0 件のコメント:
コメントを投稿