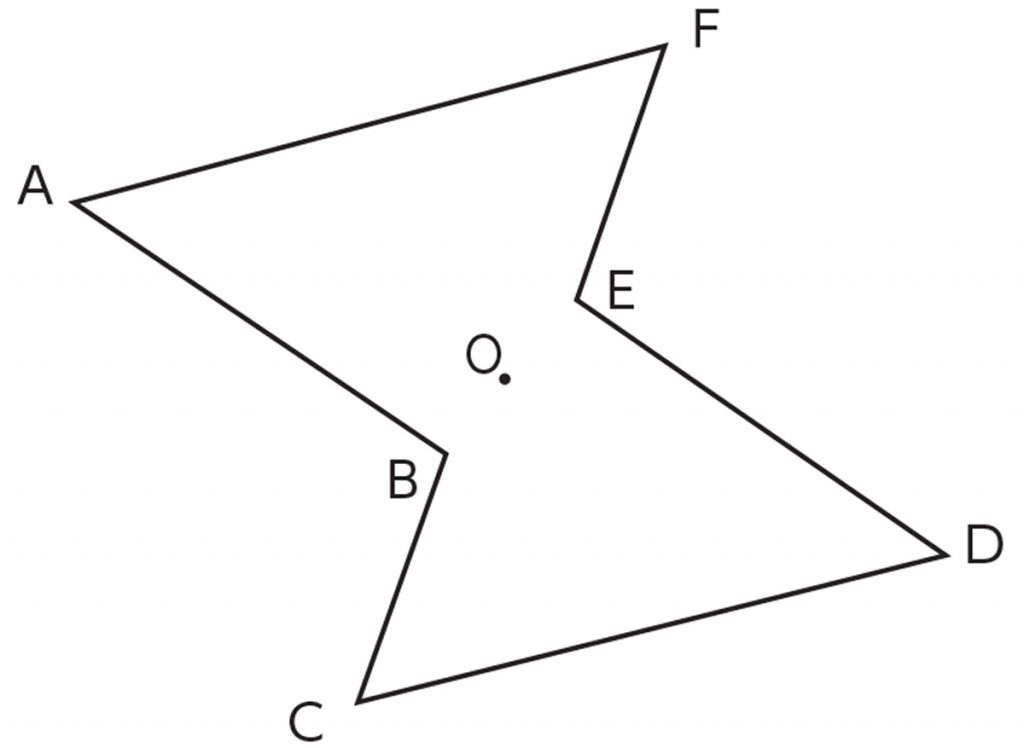
日本大百科全書(ニッポニカ) 対称の用語解説 一定点に関して2点の中点がその定点であるとき、その2点を定点に関して互いに点対称であるという。一定直線に関して2点の垂直二等分線がその定直線と一致するとき、その2点は定直線に関して互いに線対称であるという。また、一定平面に関して2の対称性を記述するのに用いる結晶点群は32種類しかな く(晶族),対称の要素は,1,2,3,4,6の5種 類の回転軸 と1(反転あるいは対称中心),2(=m,鏡 面),3,4,6(= 3/〃1)の5種類の回反軸を合わせた,10種 類に限定されま す例 えば,対称の要素として,6は31〃Zと 等しくなりま すし かし,対称の操作としては,60回 点対称を作図するのは難しい 下のような図に、点Oを中心に点対称をかくとします。 まずは、ポイントとなるかどに印をつけます。 「かどをえんぴつでぐりぐりしなさ〜い」 次に、そのぐりぐりに端から順番をつけていきます。 つけた
小6で習う 線対称と点対称 爆走おてうブログ 中学受験25
算数 点対称とは
算数 点対称とは-3 点群 31 点群と空間群 結晶の対称性は、回転・反転・鏡映と平行移動の組み合わせで表される。これらのうち、 先述のシンプルな行列で表記できるのは、回転・反転・鏡映だけである。(平行移動は並進 ベクトルで表されるが、行列による一次変換として記述することはできない) 2プロペラは1つの点を中心として 180° 回転させるともとの図形に重なるため,点対称な図形といえます。 点対称な図形では,対応する点を結ぶ線分は対称の中心を通り,対称の中心から対応する点までの距離は等しくなります。




世界一分かりやすい算数 小6 対称な図形
• 点対称操作 (point symmetry opration) :空間に固定された1点を中心として行なう対称操作 • 並進対称操作 (translational symmetry oprtion) 点対称操作における習慣 (a) 主軸(principal axis) 他の軸より高い回転対称を持つ軸であり,通常z軸あるいはc軸にとる。次の図のように,ある点を中心に180°回転させたとき,元の図形と一致する図形を点対称な図形といいます。 このとき回転の中心となる点を 対称の中心 といいます。すなわち、結晶の任意の性質が示す対称性は、結晶の点群の対称性よりも低くはなりえないのである。 これをノイマンの原理(Neumann's Principle)と呼ぶ。 ある系の対称性を考えるには、ある操作を行う前後で変化があるかないかを考えることになる。 変化が生じない場合、その操作を対称操作(symmetry operation)と呼ぶ。 結晶にある操作を行っても原子の配列が不変であれば
点対称な図形 ※右の図形は、1度(または240度)回転させると元の図形と重なりますが、 180度回転させても重ならないので、点対称な図形とはいいません。 1次の図形のうち点対称な図形はどれか答えなさい。 答え 点対称な図形を対称性の観点から 考察しようとする。 ・線対称、点対称の特徴 を見つけることができる ・平面上での2直線の位 置関係をとらえること ができる。 ・線対称や点対称の図 を見つけたり、かいた りすることができる。 ・図形の合同の意味がわ かる。点対称 の部分一致の例文一覧と使い方 空間群は、 点 群の 対称 要素を並進 対称 性 (螺旋軸および映進面)と組み合わせる。 例文帳に追加 The space groups combine the symmetry elements of the point group with translational symmetries ( screw axes and glide planes ) 科学技術論文動詞集
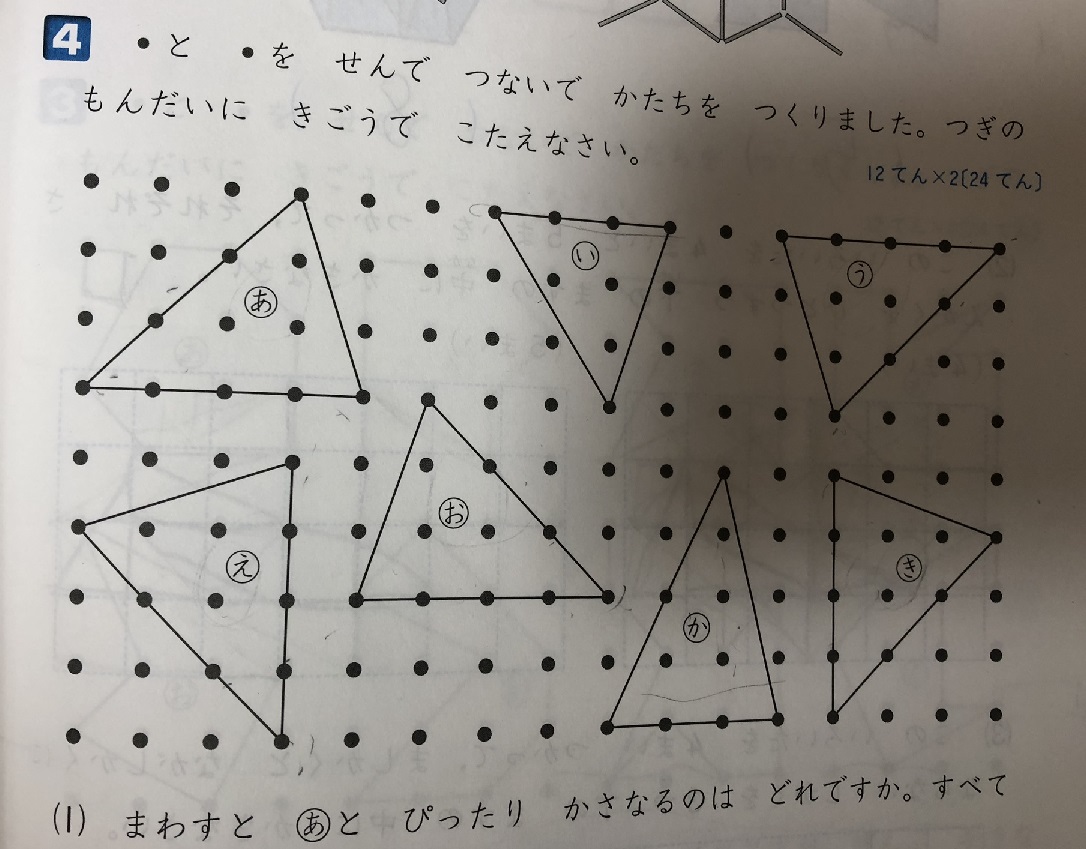
点対称(てんたいしょう、 point symmetry, point reflection )とは、対称性の一種である。 点対称な図形は、対称点(対称中心)を中心とした反転に対し不変である。3.点群 どのような対称操作によっても移動しない共通の点を有するものに存在する対称操作の集合 を点群という 点群を表す記号:Shönflies の記号 Cn 群、Dn 群、Cnv 群、Cnh 群、 Dnh 群、Dnd 群、Sn 群、 多面体群(T、Th、Td、O、Oh)など 演習 1 H2O、CH4、PF5(三方両錐)の点群は何か 2次の図形は点対称な図形です。次の問題に答えましょう。 対称な図形 ③ 1つの点を中心にして180°回転すると,もとの図形にぴったりと (1) 頂点bと重なり合う頂点を答えましょう。 (2) 頂点cと重なり合う頂点を答えましょう。 (3) 辺abと重なり合う辺を答えましょう。 (4) 角dと




標準 ある点に関して対称な点の座標 なかけんの数学ノート



スマホok 6年 対称な図形 点対称な図形のかき方 Youtube
2 二つの図形が、点・線・面などについて互いに向き合う位置関係にあること。 それぞれ 点対称 ・ 線対称 ・ 面対称 とよぶ。点対称かどうかを見分けるには・・・ 対応する点どうしを直線 で結んでみると対称の中 心が見えてくるよ 名前( ) 線対称対称の軸で2つに折ると の部分がぴったり重なる 点対称対称の点を中心に180 度回転 するともとの図形にぴったり重 なる対称要素と点群について理解しよう 内容 結晶格子 対称要素 点群 3 単位胞(Unit Cell) 結晶の持つ3次元周期構造の周期単位 4 単位胞(Unit Cell) 単位胞のとり方は一意ではない 5 結晶とは 結晶= 格子(lattice) 原子の集まり(basis) = 結晶 格子 14種(後半) 6 結晶とは 結晶= 格子(lattice) 原子の集




点対称移動 Youtube



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
ブリタニカ国際大百科事典 小項目事典 点対称の用語解説 空間の1点oがある。oを通る線分上の2点p,qがoを中心として対応する位置にあるとき,この2点は点oに対して点対称であるという。また,1つの図形が,oに関する2直角の回転移動によって自分自身に重ね合せられるとき,この図形は点oに対して点対点群Point Group 全く同じ対称要素を持つ分子は同じ点群に属す (a)C1, Cs, Ci点群 C1群:E以外に対称要素を持たない分子はC1群に属す C HOOC NH2 H3C H 18 L-アラニン 12・2分子の対称による分類 10 Cs群:E以外に鏡面σのみを持つ分子はCs群に属す N N COOHPoint 点対称・線対称・面対称 ①点対称は中点を利用する ②線対称は「中点が直線上」と「線分が直線と垂直に交わる」を利用する ③面対称は「平面の法線ベクトル」を利用する



点対称な図形 図の上半分 というのは 例えば平行四辺形やアルファベ Yahoo 知恵袋



Fdk3a7ctb5192box5b Com Es 6nen Mt Tentaishou Sakuzu Html
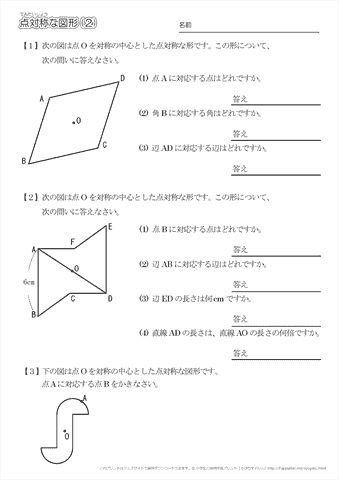
1つの点を中心にして、180度回転したとき、もとの図形にぴったり重なる図形を点対称な図形といいます。 またこの点を 対称の中心 といいます。規数学的な考え方 対称という観点から既習の図形を見直し、その性質をとらえて、図 準 形に対する見方を深める。 技能 線対称、点対称な図形をかくことができる。 知識・理解 線対称、点対称な図形の意味や性質について理解する。小6 算数「線対称・点対称」1 組 番 氏名 (1) 直線ABを対称の軸とした線対称な図形の,残りの半分をかきましょう。 (2) 右の図は直線ABを対称の軸とする線対称 A な図形です。 ア ① 対応する2つの点ウと点キを結ぶ直線ウキと ク 対称の軸は,どのように交わっていますか。 ケ イ ウ キ 答え



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生



6年算数線対称点対称図形 わかる教え方
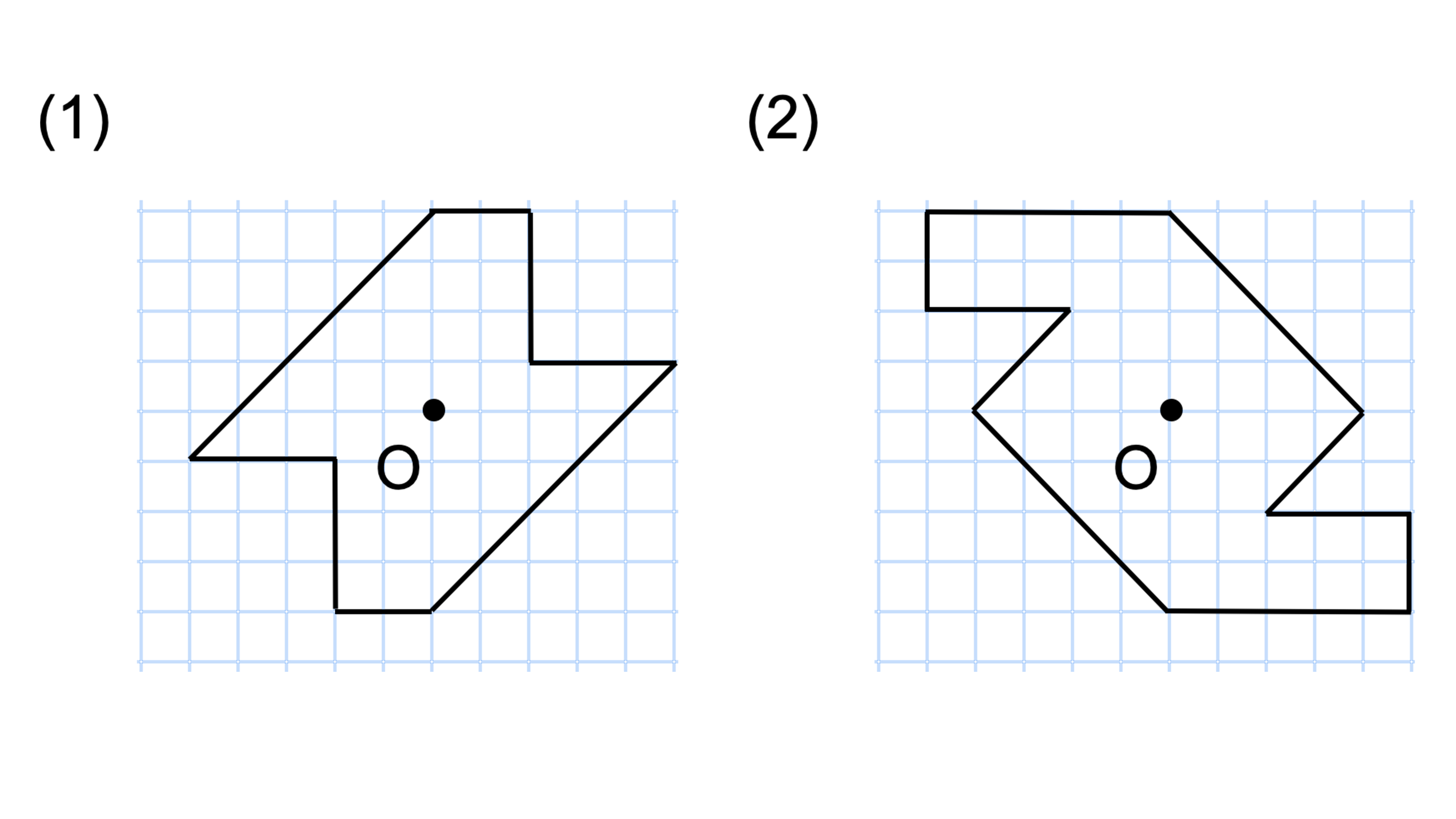
次の図のように,ある点を中心に180°回転させたとき,元の図形と一致する図形を 点対称な図形 といいます。 このとき回転の中心となる点を 対称の中心 といいます。 右の図は平行四辺形が対角線の交点を対称の中心とする点対称な図形であることを示しています。 点対称な図形では,次の図のように1つの点から対称の中心を突き抜けて向こう側に同じ距離だけ直線に関して対象な点を考えるときは ①直線lとPQとは垂直に交わる ②PQの中点Mがl上にくる を意識するようにしましょう。 ・ 3つの点が1直線上にあるとき ・ 座標上で2つの直線の交点の座標を求める問題 ・ 3つの直線の交点 直線 , 直線に対称な点 親子で解ける!大人も楽しい、算数クイズ! math channelのメンバーたちで考えた「算数クイズ」をWebでも公開! 今週は「点対称なトランプは?」の問題を出題します♪ ぜひ解いてみて下さい~! 後半に、答えも記載しています! ※こちらにPDF版もあります。



Fdk3a7ctb5192box5b Com Es 6nen Mt Tentaishou Sakuzu Html



小6算数 点対称な図形の性質 指導アイデア みんなの教育技術



0 件のコメント:
コメントを投稿