分母の有理化について 閲覧ありがとうございます。 高卒認定の試験に向けて勉強中なのですが、分母の有理化の例題について質問があります。 以下、例題と書いてある解き方です。読みづらいかと思います。申し訳ありません。 2√3/2√3を有理化せよ。 公式(ab)(ab)=a^2b^2を用有理化とは 有理化とは,分数の分母に根号 (ルート) を含む式を変形し,分母に根号を含まないようにする操作のことです.たとえば, $$\frac{1}{\sqrt{2}}$$ という分数の分母と分子に $\sqrt{2}$ をかけて, $$\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$$ とすると,分母にあった根号が除かれます.ここで重要611 有理関数の積分 ~ 部分分数の積分 次 612 1 次式の根号を含む関数の積分 上 6 積分法 前 610 有理関数の積分 ~ 部分分数分解 6 11 有理関数の積分 ~ 部分分数の積分 例 6 56 (部分分数の積分の計算例) Type 1 Type 2 Type 3 Type 4 Type 5 Type 6 これはあとの例題で示す. 例 6 57 (有理式

S計算 部分分数分解編 おいしい数学
分母が分数 有理化
分母が分数 有理化-分数の下半分にある数字を分母と言います。 そこがルート付きの数字になっていることがあります。 分母がルート付きの表記でない書き方に表現しなおすことを『分母の有理化』と言います。 分母を有理化する基本手順としては以下の通りです。 これが基本的な解き方です。 高速認定試験の分母分子に 3 をかけることによって、分母のルートが外せます: 1 3 = 1 × 3 3 × 3 = 3 3 このように、分母が n という形の分数については、 分母分子にそれぞれ n をかける ことによって分母を有理化することができます。




4 Descubre Como Resolverlo En Qanda
分母の有理化(3項) 分母を有理化する必要があるのは,分母が a \sqrt{a} a や a b p ab\sqrt{p} a b p など項の数が1つか2つであることが多いです。その場合は簡単に有理化できます。→分母の有理化や実数化を行う理由 しかし,分母が3項の場合の有理化も頻出なのでやり方を覚えておきましょう 分子の有理化って習ったけど,なんで有理化するんですか? 要するに分数にしたいから。 例えば,$\cfrac{4}{6}=\cfrac{4\times\cfrac{1}{2}}{6\times\cfrac{1}{2}}=\cfrac{2}{3}$ みたいな感じで, 分母・分子に同じ数をかけたり割ったりしてももとの数と変わらない 。分母の有理化は 簡単にするため とされているが,ここで言う 簡単 の意味はあ まり説明されていないように思われる。見ようによっては, 1 √ 2 はそのままで十分簡単だという解釈も成り立つ。そこには,数をどのように拡張する かという問題が横たわる。 中学で0および負の数を習ったが
分数の有理化 ÷ = 昔からの決まりで分母の部分は整数で表したほうがいい んだ。 その方が見た目もスッキリするよね。 分母のを工夫して整数にしてみよう。 = ×分母の有理化の方法、計算は下記が参考になります。 有理化とは?1分でわかる意味、平方根、約分、分子との関係 分母にマイナスがつく計算 分母にマイナスが付くと難しく感じる方もいますが、分子にマイナスが付く場合と変わりません。分数を割り算に置き換えて考えました。分子と 次の数を有理化しなさい。 分母に2つ項がある場合には この乗法公式の性質を利用して進めていきましょう。 分母にある に対して 1つの項の符号を変えた の式を分母分子にかけていきます。 かず先生 ちょっと計算は複雑になっちゃうけど やってる
== 分母の有理化 == 解説 分母に根号を含む式を,分母に根号が含まれない形に変形することを分母の有理化という. 有理化の長所1 _ = では,どこまでいっても計算が始まらないが, _ = の形ならば,前から順に必要なだけ求められる. 有理化の長所2 _ 3 ( 3x の形) では,簡単になるかどうか分子の有理化が役立つ例 lim n → ∞ ( n 1 − n) という極限値を計算してみましょう。 n → ∞ のとき、 n 1 も n もいくらでも大きくなるので、この式は ∞ − ∞ の不定形です。 そこで、この式を n 1 − n 1 と見て、分母分子に n 1 n をかけることでブリタニカ国際大百科事典 小項目事典 有理化の用語解説 根号を含む式,特に平方根を含む分数式の分母から,根号を取り除くように式変形する操作。分母の有理化とも呼ぶ。たとえば,は分母の有理化の操作である。qを有理数全体の集合としてαを有理数の 2乗では表されないような有理数



数学の有理化について教えてください 例えば 12 2 3 4 3の Yahoo 知恵袋




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学
分母の有理化 分母の無理数である場合に分母を有理数にするための計算操作を 分母の有理化 という.分母を有理化する目的は,計算がより簡単になる場合が多いからである. 1 a , (a > 0) の場合 分母,分子に a をかけて有理化する. 1 a = 1 × a a × a = a a 分数を有理化しよう!分母にルートが2つある時はどうしたらいいの? 2 COMMENTS om 2月 2, 19 Neko 2月 2, 19 コメントありがとうございます。 途中式を詳しくしました。 現在コメントは受け付けておりません。 前の記事 ルートの中身が大きい数の時に小さくする計算は素因数分解しないと無理数の整数部分と小数部分の求め方です。 無理数の分数処理というと有理化を思い浮かべるとおもいます。 分母が1つの場合は中学でもやっているので慣れていると思いますが、2つ以上の場合でも分母は有理化はできます。 ここでは係




平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




この問題の有理化のしかたを教えてください この問題の有理化のしか 高校 教えて Goo
分母の有理化 中学生は √1 2 (タイプ1)の形,高校生は √ 1 3− √ 2 (タイプ2)の形の分母の有理化をやる。 まあ,後はパズルのようなものがあるのみ。 (1) √ 1 5 √ 3 √ 2 (2) √ 1 6 √ 3 √ 21 (3) √ 1 5 √ 3 √ 22 (タイプ3)分母が3項以内だと,分母の有理化をa2 −b2 の公式で何回かやる 平方根 (分母の有理化) 中3数学 分数の上下に同じ数字を掛けて、分母のルートを外す作業です。 ルートの計算がしっかり定着していれば決して難しくはないですが、約分やルートを簡単にできるときは必ずすることだけは注意しましょう。有理化 分母に √ のある分数を整理し,分母に √ がない式に変形することを分母の有理化という。 例題1 2 √ 7 を有理化しなさい。 分子と分母に √ 7 をかけ算すればよい。 2 √ 7 = 2 × √ 7 √ 7 × √ 7 = 2 √ 7 7 答 例題2 3 √ 6 を有理化しなさい。 分子と分母に √ 6 をかけ算すればよい。 3 √ 6




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学
まずは分母の有理化の定義から。 「分数において、分母に根号を含んでいた場合、根号を含まないように変形する」ことです。 分母に根号を含んでいると、分数同士で足したり引いたりするのに支障をきたしてしまいます。 よってこの考え方は、本分野では必須です。確実に身につけま 分母の有理化 分母のルートと同じものを分母、分子にかける。 1 a = 1× a a × a = a a 分母に式がある場合、和と差の積を利用する。 和と差の積:(xy)(xy)=x 2y 2 1 a b = 1×(a − b) (a b)×(a − b) = a − b ab 分母を有理化せよ。 15 2 3 12 7 5 1 3 5 7 ①分母と分子に 3 をかける。 ②分母と分子に 7 − 5 分母の有理化について解説していきます。中学数学では分母は単項式のみでしたが、高校数学からは多項式も出てきます。計算方法をしっかりと理解しできるようになりましょう。 教科書より詳しい高校数学 高校数学Ⅰ 数と式 集合と論理 2次関数 図形と計量 データの分析 高校数学A




複雑なルートの分数の有理化のやり方と問題 理系ラボ
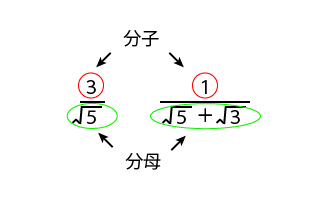



有理化 もう一度やり直しの算数 数学
どっちも簡単な話な。 まず分数の方。 約分って知ってるやんな? 分母と分子、下と上、同じ数字で割れたら割るっていうやつ。 それを 逆走 させんねん。数学では、分数の分母にはルートを書かないというルールがあります。 計算の結果、分母にルートが入ってしまった場合には、分母を有理化して、ルートをはずしましょう。 この"有理化"が今回の学習のポイントです☆ ページトップへ戻る これ、知っ得!? 分数のルールについて確認し電験三種の数学 分母の有理化 2つの基本を押さえる 理論の計算において分母の有理化でつまずかない なぜ分母を有理化する必要があるのでしょうか?あるサイトに「採点者が楽だから」なんて笑い話もあります。しかし、理科ではより実態に近い数字を出すことが必要ですので、分母の無理数
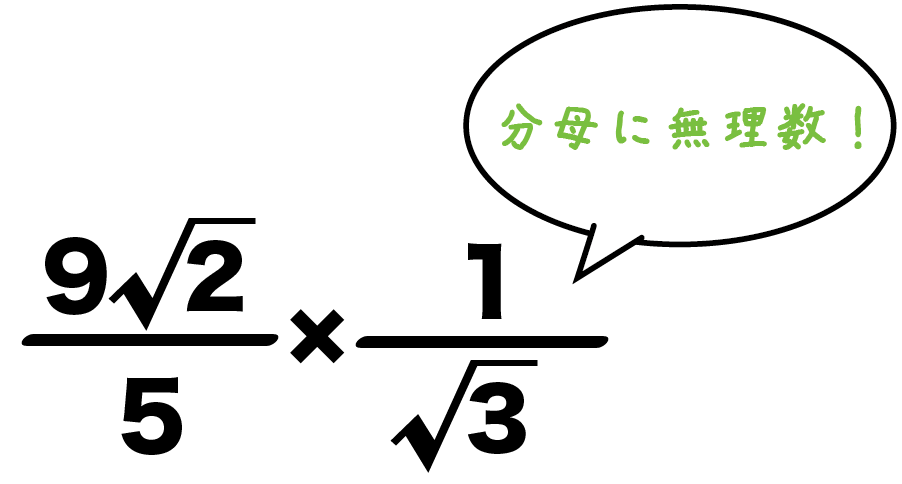



ルート分数の掛け算の計算方法がわかる3ステップ Qikeru 学びを楽しくわかりやすく




分母の有理化
Mixi数学科 教師 講師 分母の有理化は必須? 分母の有理化を必ずやるように指導しているところが多いようですが、中学の教科書を見ても、1/√2 の近似値を求めるときに√2 /2の方が楽とは書いてあるけど、常に有理化するように、とは書いてありません。「分母が無理数である分数」 に対して,分母と分子に同じ数をかけて「分母が有理数である分数 」に 「分母を有理化できる場合はしないといけない」という主張を盲目的に信じていたため,無理のある主張をしておりました。複数の方からご指摘をいただき,年1月に改めてじっくりA評価 : 分数は、分母分子に同じ数をかけても値が変わらないという性質と、平方根は、 2乗すると有理数になるので分母を有理化することができる。 B評価 : 分母分子に § 2をかけることで、6 § 2 は 6 § 2 2 になり分母を有理化することができる。




数学 分母にルートの分数がある場合の計算を教えてください 下の計算 数学 教えて Goo




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




2 項展開 分母の有理化 近似分数




平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




分母に項が3つある場合の有理化 高校数学の美しい物語




数学 質問解答 分母の有理化って どうやればいいの 平方根 中3 中学数学 質問ありがとうございました 行間 ぎょうのあいだ 先生




S計算 部分分数分解編 おいしい数学




分母の有理化 Youtube




乗法公式を利用した分母の有理化 Youtube
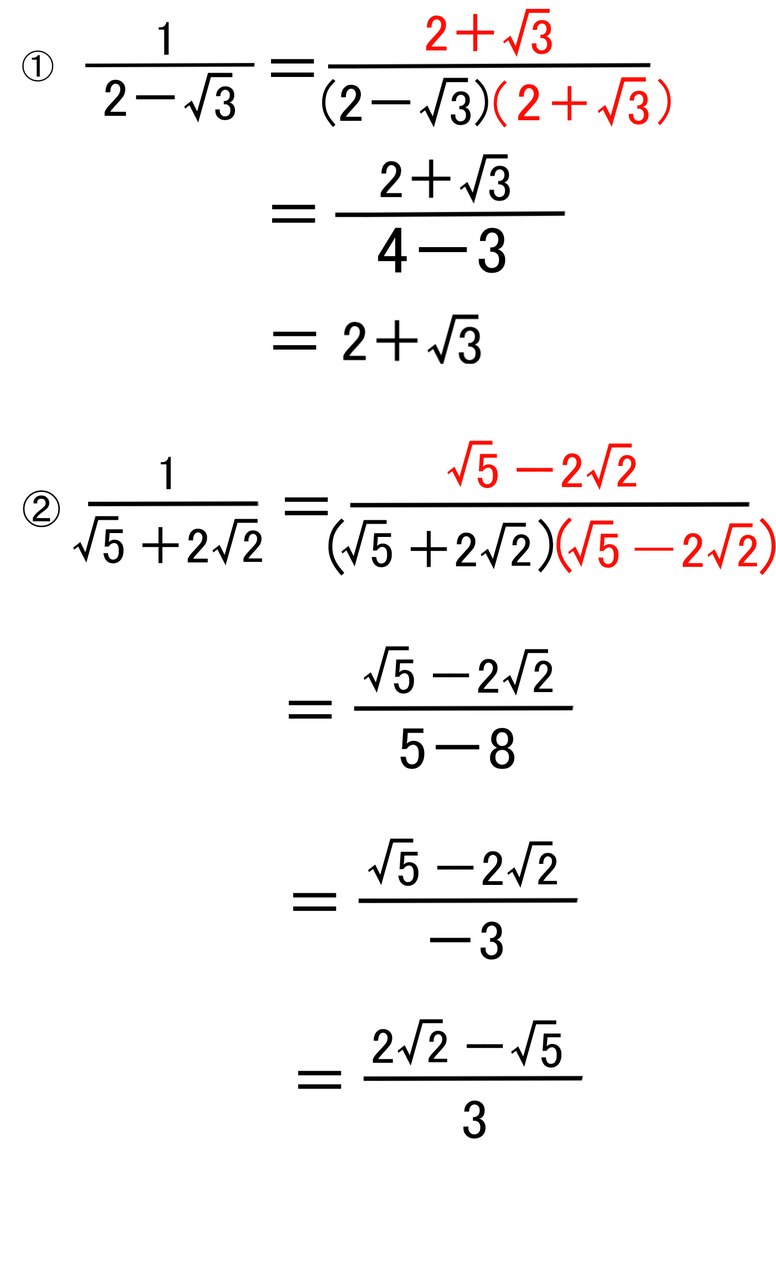



平方根 5 分母の有理化 バカでもわかる 中学数学
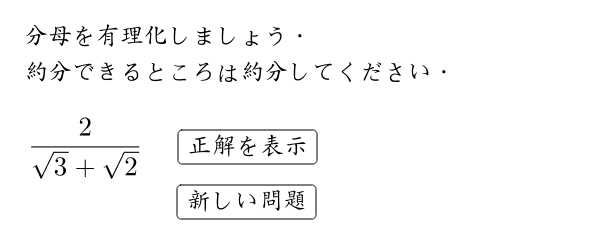



有理化2 Geogebra




有理化
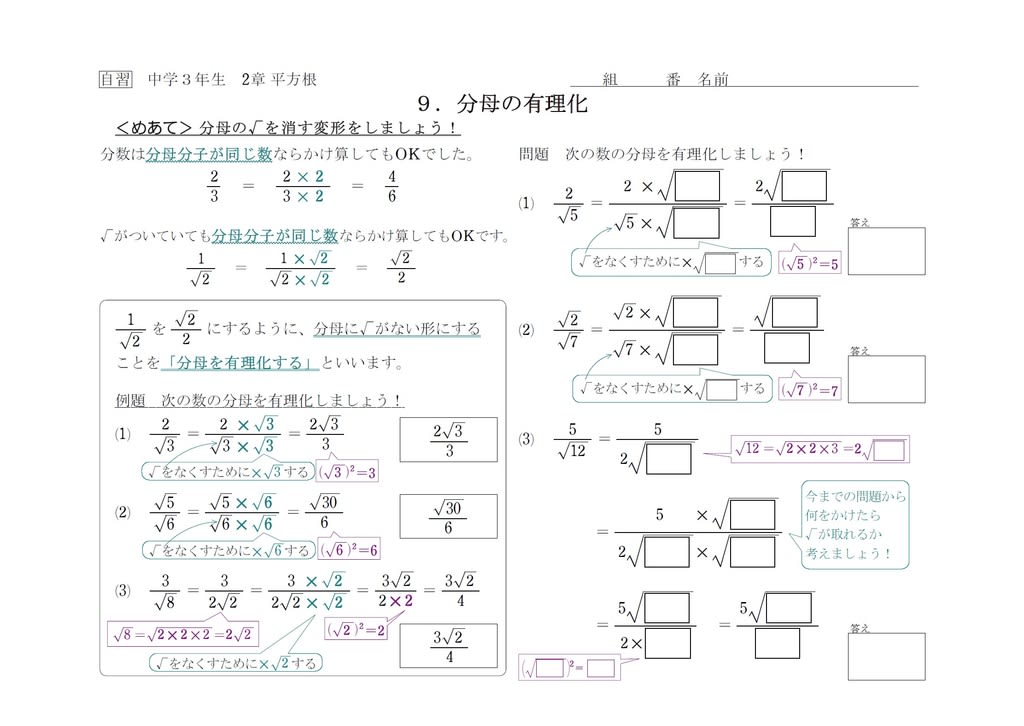



中3自習 平方根4 有理化 中学数学の勉強に




ルートの値を代入する問題 色んな知識を使う良い問題です 中学や高校の数学の計算問題
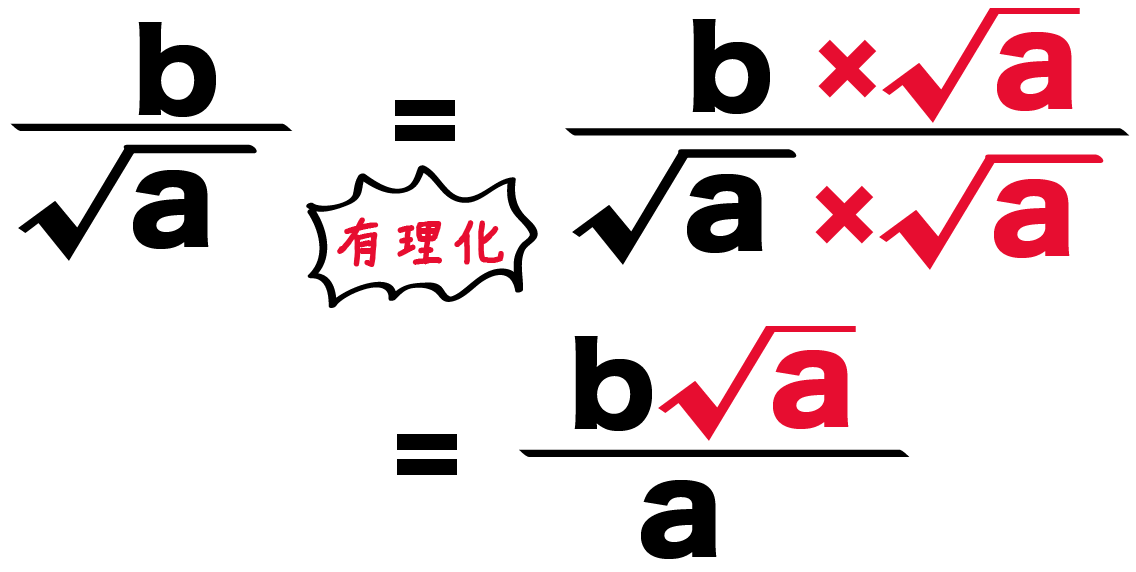



平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



48s96ub7b0z5f Net Kongou Kyokugen




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ




高卒認定試験数学の平方根 分母の有理化の解き方を解説 坂田先生のブログ




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ




中学数学 平方根 のコツ 有理化 加減乗除 展開




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ




平方根 有理化 チーム エン




この問題で 分母に をつけて有理化するときに 6 2 の方に をつけるやり Clear



ルートの有理化についてこちらの問題が約分が出来ない理由を教えてください Yahoo 知恵袋




数学 平方根 分母の有理化 Youtube



有理化について質問があります この分数を有理化するとき 5 Yahoo 知恵袋




式を分けた時に出てくる分数部分をひと目で見つけ出す方法ってないんですか 私は馬鹿なの Clear




複素数の分数の実数化 分母の有理化の複素数版 Irohabook




分母有理化的定义是什么 快资讯




2つの解法 3乗根の有理化 数学ii 指数関数と対数関数 Youtube




高校数学 数 13 ルート シリーズ 有理化編 Youtube




分母の有理化 問題 Youtube




実数 ルート を有理化する意味はこれでわかる 分母に がngの巻 Vol 9 3回読めば 絶対理解できる看護受験数学 Kazアカデミー 大阪の看護学校 看護予備校



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




三項の有理化 高校数学 Youtube




有理化なんですけど なんでマイナスをつけるんですか 2枚目が私の考えたやつです Clear



急募です この問題は有理化の時になぜ 上の分母にマイナスをかける Yahoo 知恵袋
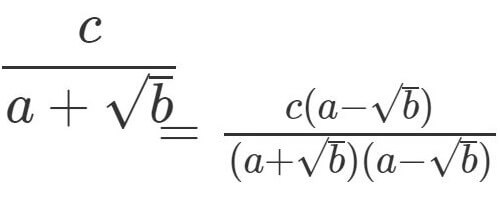



数学 有理化は必ずするべきか もう一人のy君




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ




ルートの計算で分数の分母を有理化しないといけない理由とは さびねこ中学校



平方根の割り算は 1分でわかる計算 割り算の問題とやり方 有理化 分数との関係
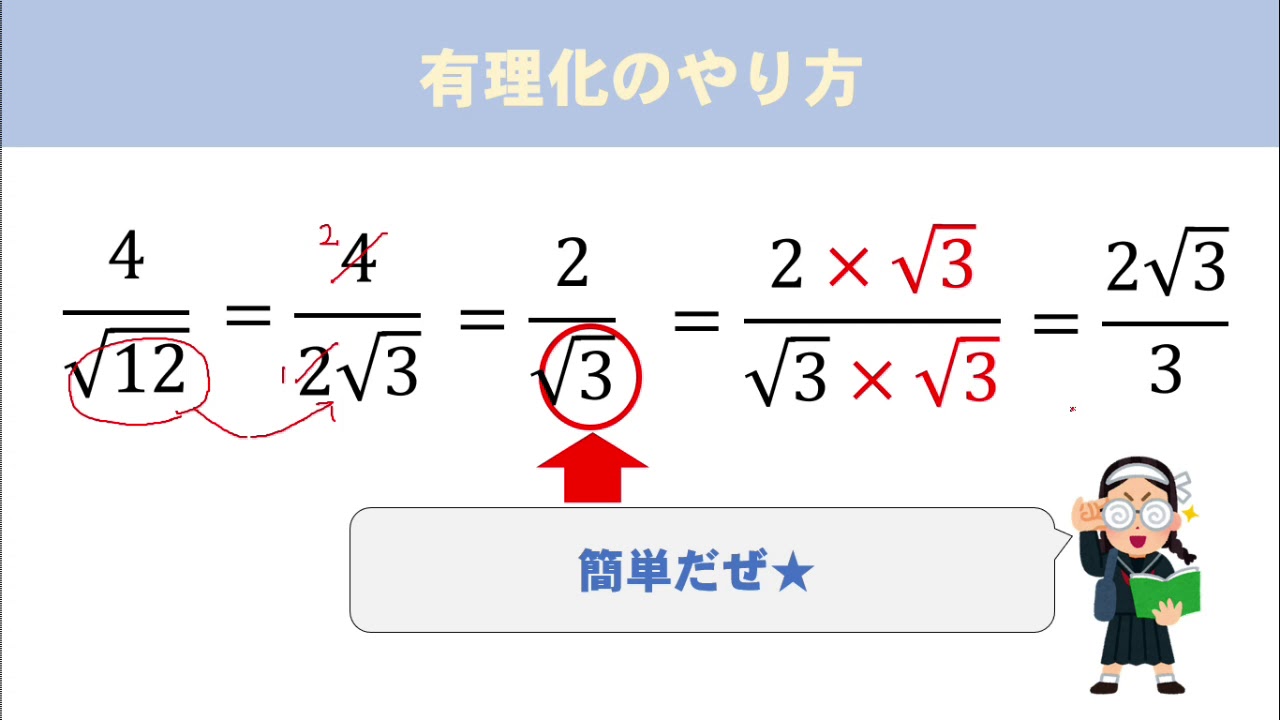



平方根 分母の有理化のやり方はこれでバッチリ 数スタ
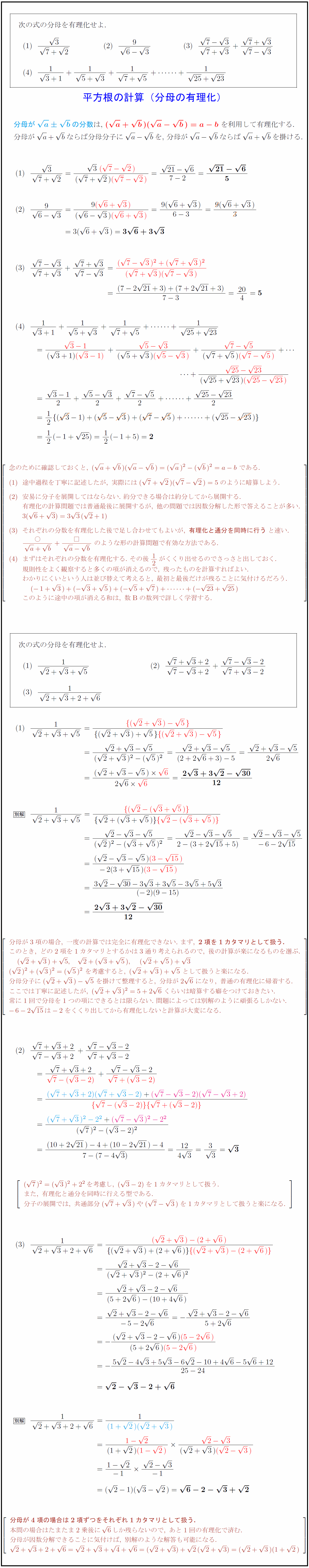



高校数学 平方根の計算 分母の有理化 受験の月



1




分母の有理化の方法 数学の偏差値を上げて合格を目指す



平方根 分母の有理化のやり方はこれでバッチリ 数スタ




平方根 ルート の重要な計算方法まとめ 数学fun



平方根 分母の有理化のやり方はこれでバッチリ 数スタ




平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



Math 超簡単 有理化 分母に根号がない形にする 働きアリ




中学数学 平方根 のコツ 有理化 加減乗除 展開



この有理化の計算のところなんですが 分数を有理化するとき分母と同じ数を掛け Yahoo 知恵袋




8 3 分母の有理化 イ弋マ本ゼミナール




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ



Q Tbn And9gcqf Morlw6cxdlfm9ekiq1ofry1mzj8ja8btamlmt2mbn1rfilc Usqp Cau
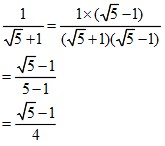



Math 超簡単 有理化 分母に根号がない形にする 働きアリ




平方根 分母の有理化のやり方はこれでバッチリ 数スタ




有理化の計算 やり方は 分母のルートを分子にかけるだけ 中学や高校の数学の計算問題



1




複素数の分数の実数化 分母の有理化の複素数版 Irohabook




Descubre Como Resolverlo En Qanda




有理化




高校数学 無理関数の積分2パターン 分母の有理化と根号丸ごと置換 受験の月
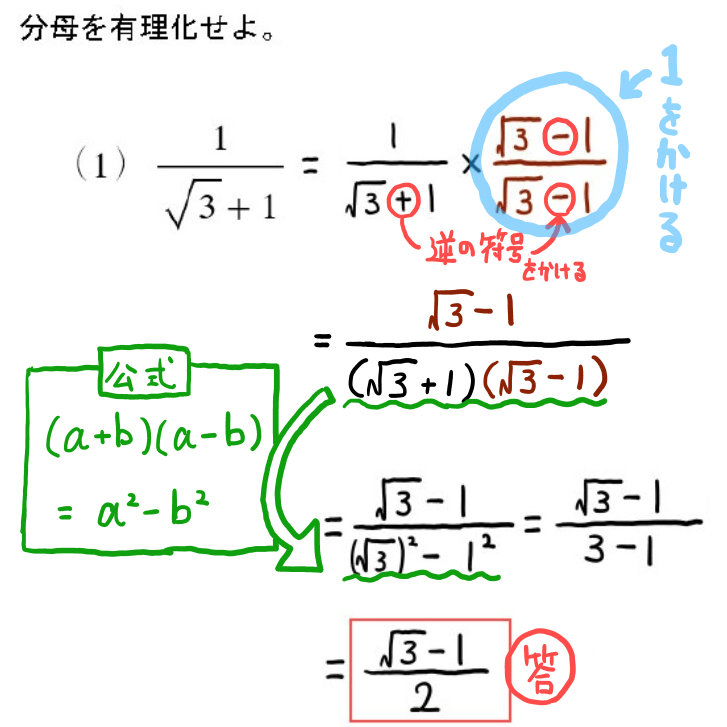



高卒認定試験数学の平方根 分母の有理化の解き方を解説 坂田先生のブログ




数学 定期テストに出題される分母を有理化する問題 大学入試数学の考え方と解法
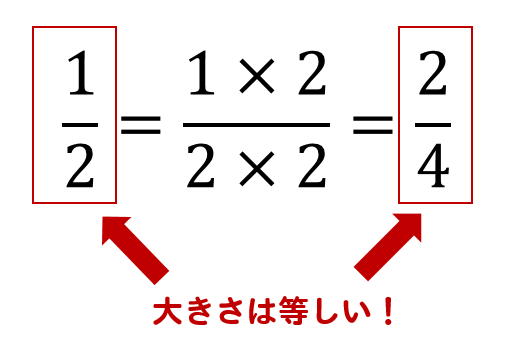



平方根 分母の有理化のやり方はこれでバッチリ 数スタ




分数の分母を有理化する問題です 答えがなくて分からないので教えてください Clear
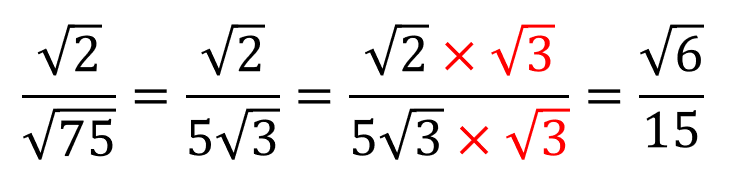



平方根 ルート の重要な計算方法まとめ 数学fun




数学 分母にルートの分数がある場合の計算を教えてください 下の計算 数学 教えて Goo




平方根と指数 どこかの街の電気屋




有理化の分数計算 看護受験の必須 数学の公式を確認テスト Vol12 Kazアカデミー 大阪の看護学校 看護予備校




数学解説13時間目 数学i 分母の有理化 フリーランス教師の数学解説日記
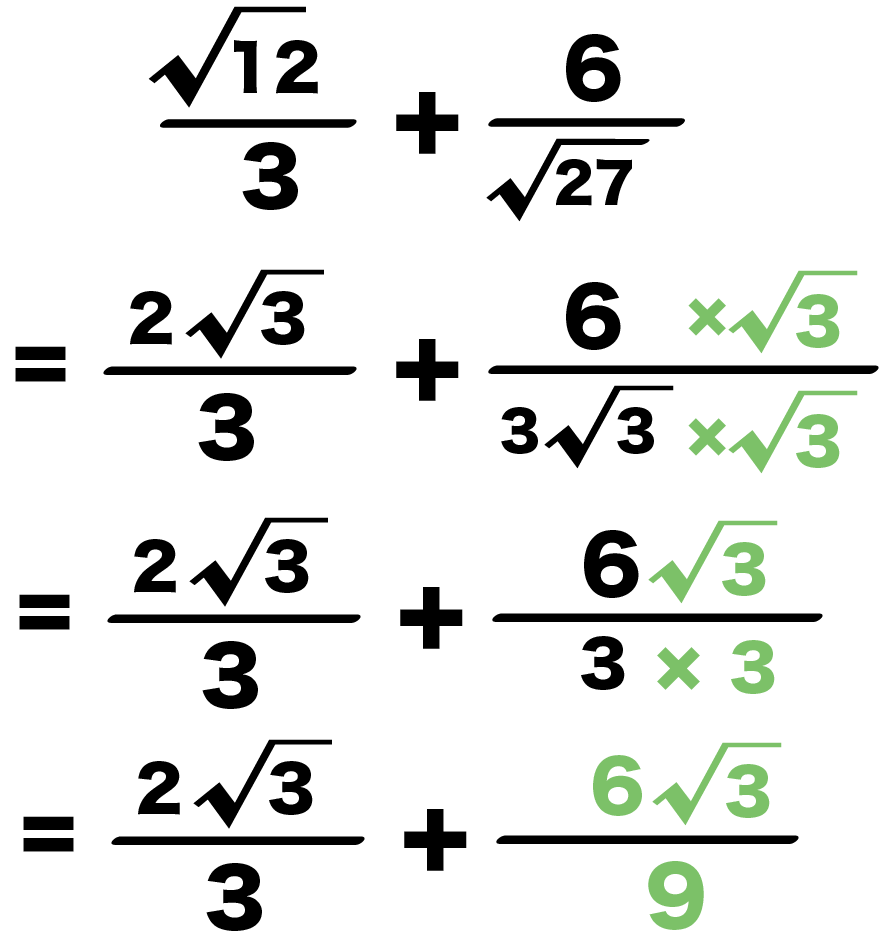



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




ルート分数の有理化 項2つ3つある場合は やり方まとめ 高校生 中学数学 理科の学習まとめサイト




4 Descubre Como Resolverlo En Qanda




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学
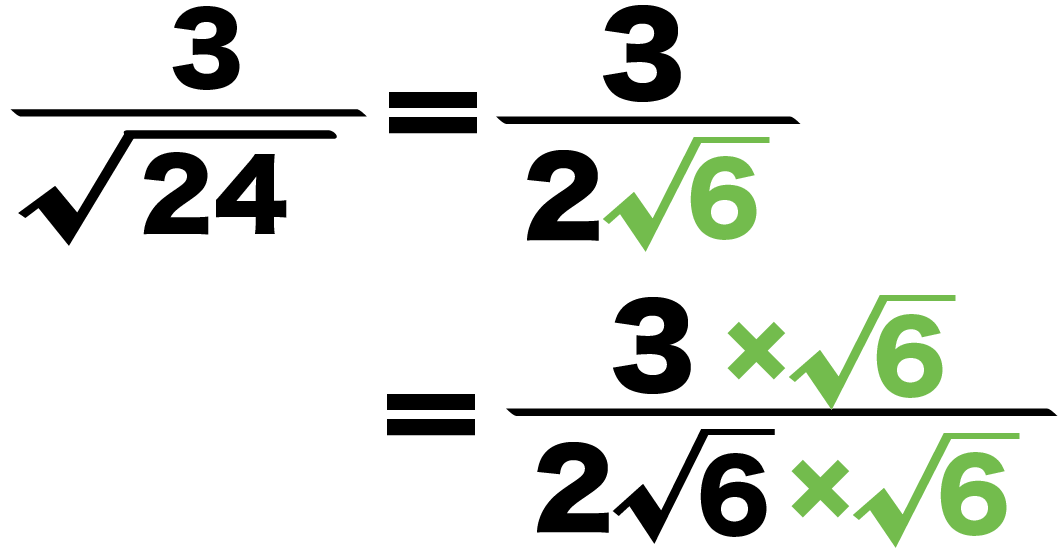



平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




数学 中3 19 有理化 Youtube




バカでもわかる 中学数学 平方根




平方根 ルート の重要な計算方法まとめ 数学fun



1
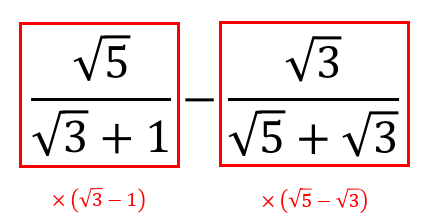



ルートの分数計算 問題解説で完全マスターだ 数スタ




中学数学3年 平方根の計算 加法 減法 乗法 除法 と分母の有理化 受験の月




高卒認定試験数学の平方根 分母の有理化の解き方を解説 坂田先生のブログ




ルートの中を簡単にする と 分母の有理化 を比べる とちぎeライブラリ




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




高校数学 分母の有理化2 映像授業のtry It トライイット




分数を有理化しよう 分母にルートが2つある時はどうしたらいいの さびねこ中学校




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ




4 Descubre Como Resolverlo En Qanda




複雑な分母の有理化 Youtube




有理化 をclasspad Netで自動計算 Mathapp Days



0 件のコメント:
コメントを投稿